Para resolver los problemas a partir de los datos existentes, es importante en primer lugar, encontrar la expresión matemática de la función que represente el problema y cuyos valores máximos o mínimos se desean obtener.
Si la expresión matemática contiene varias variables, deberá plantearse en función de una sola; las condiciones del problema deben aportar suficientes relaciones entre las variables, para poderse expresar a todas ellas en función de una sola variable independiente.
Una vez que se tenga la función en la forma Y=f(X), se aplican las normas ya estudiadas.
En muchos problemas prácticos resulta muy sencillo identificar cuales valores críticos dan máximos o mínimos; y en consecuencia, ya no será necesario aplicar el procedimiento completo.
Es conveniente construir la grafica que represente la función en cuestión, a fin de verificar los resultados obtenidos.











 , y usando la expresión
, y usando la expresión  donde en este caso,
donde en este caso, 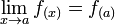 , y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función
, y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función  es continua en el punto
es continua en el punto  se define como sigue:
se define como sigue: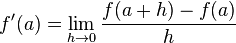 ,
, ,
,
