Condiciones de continuidad de una función

Una función continua es aquella cuya regla de correspondencia asigna incrementos pequeños en la variable dependiente a pequeños incrementos de los elementos del dominio de dicha función, es decir, , y usando la expresión Δy + y = f(Δx + x), queda donde en este caso, f(x) = y. Ello quiere decir que 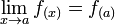, y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con
es continua en el punto a.

Se tiene que la derivada de la función en el punto se define como sigue:

,

 

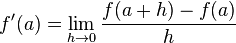También puede definirse alternativamente la derivada de una función en cualquier punto de su dominio de la siguiente manera:

,

La cual representa un acercamiento de la pendiente de la secante a la pendiente de la tangente ya sea por la derecha o por la izquierda según el signo de . El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.
No obstante su aparente diferencia, el cálculo de la derivada por definición con cualquiera de los límites anteriormente expresados, proporciona siempre el mismo resultado.
El conocimiento de todas las expresiones anteriores y su significado representan el acercamiento epistémico más completo posible en torno a la definición de derivada, y con ello, al aspecto esencial del cálculo diferencial.